[DLS]Neural Networks and Deep Learning(1)

Andrew Ng 교수님의 Coursera - Deep Learning Specialization 첫번째 강의입니다.

강의 순서

1. Neural Networks and Deep Learning
2. Improving Deep Neural Networks: Hyperparametertuning, Regularization and Optimization
3. Structuring your Machine Learning project
4. Convolutional Neural Networks
5. Natural Language Processing: Building sequence models

Neural Network

기본적인 NN에서 여러 개의 layer가 존재할 수 있다. input layer와 output layer 사이는 hidden layer이다. 일반적으로 해당 layer가 무슨 역할을 하는지 생각할 필요 없이 Fully connected하여 신경망에게 맡기면 된다.

Supervised Learning 지도 학습

학습 데이터의 Input(x)와 Output(y)가 mapping 되어 있어야한다.

Input값(문제)과 Output 값(정답)을 모델에게 가르쳐줌으로써 supervise 함

Structured Data vs Unstructured Data

• Structured Data
  • DB Table과 같이 각 속성 별 값들로 구조화된 데이터
  • Computer 가 이해하기 쉬움
• Unstructured Data
  • Audio, Image, Text 와 같이 정해진 format이 없는 데이터
  • 사람이 이해하기 쉬움
  • Neural Network가 나옴으로써 컴퓨터도 이해하기 시작

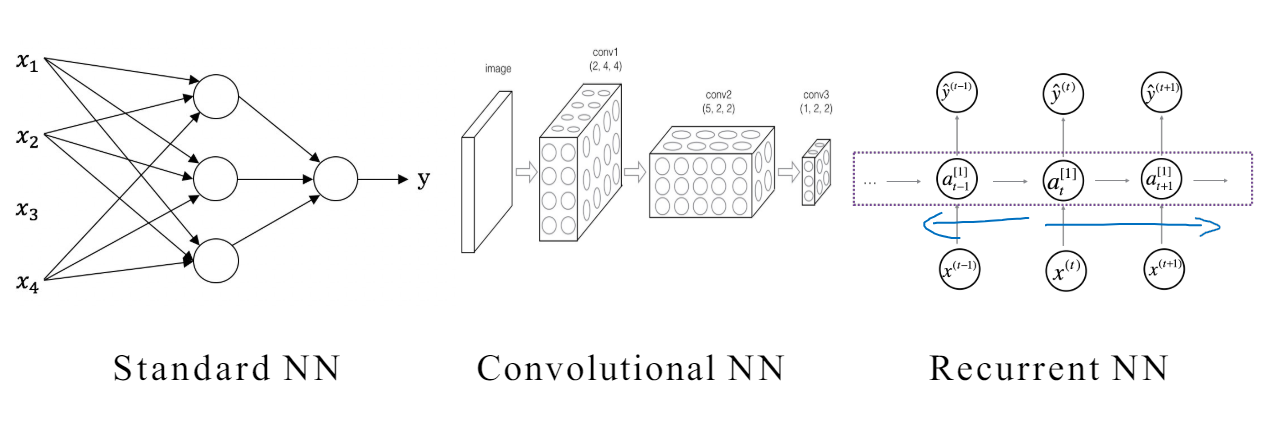
ReLU 함수의 장점

기존 sigmoid 함수는 지수 계산을 해야하는 것에 비해 ReLU는 계산 과정이 매우 단순하다. 이는 계산 효율성을 증가 시키고 학습 과정을 가속 시킨다.

학습이 빠르면 만든 모델에 대한 Experiment 시간이 감소한다는 뜻이고 이는 실험결과를 토대로 새로운 Idea를 더욱 빠르게 시도해볼 수 있다는 뜻이다.

이외에도 Gradient 소실 방지를 해주는 등의 장점이 있다.

Logistic Regression

이진 분류 문제에서 출력은 0 or 1 이 나와야한다.

\[\hat{y} = w^Tx + b\]

선형적으로 연결된 위 식을 0과 1로 변환하기 위해 sigmoid 함수를 사용한다.

Sigmoid

\[\sigma(z) = \frac{1}{1 + e^{-z}}\]

0 일 때는 0.5, 양의 무한은 1로 수렴, 음의 무한은 0으로 수렴한다.

이러한 함수를 씌워 이진 분류를 해결할 수 있다.

Loss(error) Function

• 직관적인 예 - MSE(Mean Squared Error)

\[L(\hat{y}, y) = \frac{1}{2}(\hat{y} - y)^2\]

계산한 결과가 실제 값과 얼마나 차이가 나는 지를 포함해야한다.

하지만, 이는 local optimal을 가지게 되게 때문에 convex한 함수를 써야한다.

• Cross Entropy

$L(\hat{y}, y) = -(y\log\hat{y} + (1 - y)\log(1 - \hat{y}))$

Cost function

손실 함수는 단일 데이터에 대한 손실을 측정하는 반면 학습은 여러 데이터를 한번에 진행한다. 학습하는 전체 데이터에 대해 손실을 측정하는 함수를 Cost fucntion J 라고 한다. 각 데이터의 손실의 평균으로 계산한다.

\[J(w, b) = \frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)}, y^{(i)}) = -\frac{1}{m}\sum_{i=1}^my^{(i)}\log\hat{y}^{(i)} + (1 - y^{(i)})\log(1 - \hat{y}^{(i)})\]

• w: Weight matrix
• b: bias(마지막에 더해지는 스칼라 값)
• m: (x, y) 데이터 쌍의 개수

Gradient Descent

\[w := w - \alpha\frac{\partial J(w, b)}{\partial w}\] \[b := b - \alpha\frac{\partial J(w, b)}{\partial b }\]

• $\alpha$ : learning rate

해당 parameter로 편미분한 기울기를 원래 값에서 빼면 비용이 낮아지는 방향의 값을 얻을 수 있다.

Back propagation

Computation Graph를 그리고 $J(\hat{y}, y)$을 각 parameter로 미분한 값을 Chain Rule을 통해 구한다.

\[\frac{\partial J}{\partial w} = \frac{\partial J}{\partial z} \frac{\partial z}{\partial w}\]

• Logistic 회귀에서 손실함수를 $z$로 미분한 값은 $a - y$ 이다.
  • cross entropy를 미분한 값에 sigmoid를 미분 한 값을 곱하면 해당 값이 나온다.

Vectorization

각 w(weight), z(선형 함수 결과), a(활성 함수 결과)에 하나씩 미분을 적용하는 것은 오래 걸린다. 그렇기에 for문으로 하나씩 계산하는 것이 아닌, numpy를 사용하여 한번에 행렬연산으로 수행한다.

이렇게 벡터, 행렬 연산을 하고 for 문을 없애는 걸 Vectorization이라고 한다.

이렇게 Vectorization된 역전파 과정에서 $dZ$는 그대로 $A^{[L]} - Y$이지만 $dW$나 $db$의 경우 $\frac{1}{m}$이 붙는 모습을 볼 수 있는데, 갑자기 왜 붙는지 헷갈릴 수 있다.

이건 행렬의 shape를 고민해보면 이해하기 쉽다. $dZ$들의 경우 $Z$와 같은 크기일 테니 $n^{[L]} \times m$ 이다. 이를 사용해 $dW$를 만들어야하며, chain rule에 따라 $dZ$ 값에 이전 층의 $A$ 값을 곱하게 된다. 이때 $m$이 사라지고 $n^{[L]} \times n^{[L - 1]}$ 이 된다.

즉, 행렬 연산에 따라 input size $m$ 개 만큼이 동시에 계산되어 더한것이므로 $\frac{1}{m}$이 생겨있는 것이다. 원리에 따라 하나씩 뜯어보면 당연하지만 수식만 갑자기 봤을 때 누구는 안 나누고, 누구는 나누니 이상함을 느낄 수 있다. 주의하자.