[DLS]Hyperparameter Tuning, Regularization and Optimization(2)
Andrew Ng 교수님의 Coursera - Deep Learning Specialization 두번째 강의입니다. 이번 게시글은 학습을 가속화할 수 있는 Optimization Algorithm을 다룹니다.
Optimization
학습 속도를 빠르게 하기 위한 기법이다 optimizer에는 다양한 종류가 있고 각각의 장단점이 있다.
mini-batch gradient descent
전체 훈련 데이터 세트를 batch 라고 한다. 그리고 데이터 세트의 일부를 선택한 것을 mini-batch라고 한다. 한번의 gradient descent에 전체 batch 대신 mini-batch를 사용하는 것을 의미한다.
💡 epoch
1 epoch은 전체 batch를 1번 학습 한 걸 의미한다. mini-batch를 사용하면 ${m}/{mini-batch-size}$의 학습 후 1 epoch이 지난다.
SGD(Stochastic Gradient Descent)
mini batch size가 1인 gradient descent이다.
수렴이 불가능하고 헤매지만, 속도가 매우 빠르다. 하지만 한번에 하나의 데이터만 사용하므로 Vectorization의 장점을 잃고 병렬 처리의 속도 향상을 얻지 못한다.
실제로는 SGD나 BGD 말고 1 ~ m 사이의 적당한 값을 mini-batch size로 선택하여 사용한다.
mini-batch size
- small train set: $m$ ; batch gradient descent
- Typical case: 64, 128, 256, 512 등 2의 지수
- memory가 한번에 잘 읽을 수 있다.
- CPU/GPU memory에 맞추자
Exponentially Weighted Averages
\[V_t = \beta V_{t-1} + (1 - \beta)\theta_t\]- $\theta_t$: t 시점의 값
- $V_t$: t 시점의 계산된
Exponentially Weighted Average값 - $\beta$: 파라미터(결과를 $\frac{1}{1-\beta}$ 개의 평균과 비슷하게 만들어줌)
매우 적은 양의 메모리와 연산으로 구현이 가능하다. 정확도는 약간 손해를 보더라도 효율적인 점에 착안하여 머신러닝에서 많이 쓰인다.
v = 0
for theta in values:
v = beta * v + (1 - beta) * theta
Bias correction
v가 0으로 초기화되어서 초반에 0에 근접한 값이 나오게 된다. 이 bias를 수정하기 위해 계산된 v에 correction 절차를 추가한다.
\[V_t = \frac{V_t}{1-\beta^t}\]$V_t$를 $\theta_{1..t}$ 들로 모두 풀었을 때 각 항들의 계수를 전부 더하면 $1-\beta^t$가 나온다.
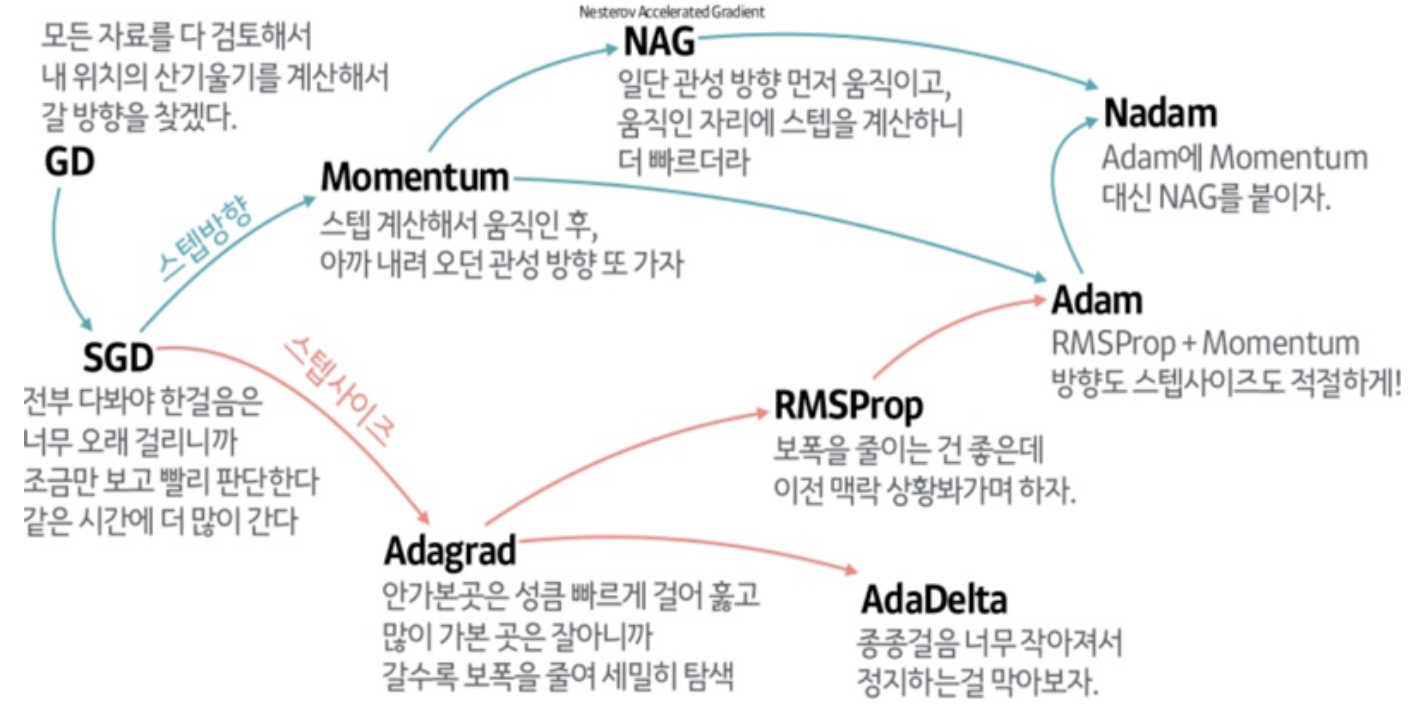
Momentum(with Gradient Descent)
Gradient Descent에서 optima를 찾아가는 과정 중 불필요한 oscillation 진동이 일어나곤 한다. 그렇더라도 step이 지나갈 수록 분명 optima 방향으로 가고는 있을 테니 전체적인 진행 방향을 고려해 최대한 비틀거리지 말자! 라는 개념이다. 최근의 이동 방향에 따라 관성(momentum)이 적용되어 나아가게 된다.
바로 여기서 Exponentially Weighted Averages이 사용된다. step마다 추가로 각 parameter의 gradient에 대해 EWA를 계산하고 그 방향으로 나아간다.
$\beta$를 마찰에 따른 속력 변화율, $V$를 기존 속력, $dW$를 가속도라고 생각하면 이해하기 쉽다.
$\beta$는 보통 0.9로 많이 한다.
이 경우 10회 이후 값이 정상화 되므로
bias correction은 잘 쓰지 않는다.
RMSprop
Root Mean Square Propagtion 의 약자로 제곱(Square) 평균(Mean)의 제곱근(Root)에 반비례한 비율 만큼 업데이트한다.
많이 움직인 parameter는 이미 적절한 값에 도달했을 가능성이 크다. 따라서 적게 움직였던 parameter들의 보폭을 키우고, 많이 움직인 parameter들은 보폭을 줄인다.
여기서 움직임 척도는 기울기들의 제곱 평균을 이용하며 Exponentially Weighted Averages를 활용해서 계산한다.
- 더 큰 $\alpha$를 사용할 수 있는 장점이 있다.
- $S_{dW}$가 너무 작은 값이 되면 발산될 수도 있으니 분모에 아주 작은 $\epsilon$을 추가로 더하였다.
Adam(Adaptive Moment Estimation)
Momentum과 RMSProp을 합쳐서 뛰어난 optimizer가 탄생했다! 1차 moment로 지나온 경로에 대한 관성을 가지고, 2차 moment로 이동량에 대해 적응하여 적절한 보폭을 가지게 된다.
- $\alpha$: 학습률은 튜닝이 필요하다.
- $\beta_1$: 주로 0.9
- $\beta_2$: 주로 0.999
- $\epsilon$: $10^{-8}$ 튜닝 필요 없음
epsilon의 위치가 루트 내부인지 아닌지 다른 블로그들을 보면 헷갈리는데 원 논문 ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION을 보면 밖에 있는게 맞다.
Learning rate decay
처음엔 크게 돌아다니며 optima 근처로 가고, 이후 줄어든 학습률로 optima에 수렴할 수 있다.
또한 mini-batch에서는 수렴하지 못하고 optima 근처에서 배회하게 된다. 따라서 학습률을 점점 작게 만들면 optima의 근처에서 넓게 배회가 아닌, 맴돌게 할 수 있다.
\[\alpha=\frac{1}{1+decayRate \times epochNumber} \cdot \alpha _0\]확실히 도움이 되지만 중요도는 낮은 편이다.
Other decay methods
\[\alpha=0.95^{epochNumber} \cdot \alpha _0\] \[\alpha=\frac{k}{\sqrt{epochNumber}} \cdot \alpha _0\]구현엔 여러가지 방법이 있다.
Local Optima & Saddle Point & Plateaus
손실 함수가 Convex 볼록하지 않아서 어딘가 Local Optima에 갖힐 수도 있다.
하지만 parameter가 매우 많은 고차원에서는 Local Optima보다 Saddle Point, Plateaus의 위험이 커진다. Local Optima는 모든 매개변수가 아래로 볼록해야하는데 이런 부분을 만날 확률보다 위든 아래든 기울기가 전부 0인 구간을 만날 확률이 더 높기 때문이다.
Saddle Point: 안장점으로 말 안장 처럼 생긴 지점을 말한다. 즉, 하나는 위로 볼록 다른 하나는 아래로 볼록한 지점이다.Plateaus: 고원이란 뜻으로 주변부분이 전부 0에 가까운 평평한 지점을 말한다.
이런 구간을 만나면 기울기가 0에 가까워져 아주 천천히 움직이게 되고 학습이 매우 느려지게 된다. 이 구간들을 쉽게 탈출하기 위해서 Optimization Algorithm이 필요하다.
Adam의 경우를 생각해보면, 움직임이 적으면 자동으로 보폭을 키우고, 이전의 gradient 정보를 활용해 고원 구간을 빠르게 탈출할 수 있는 등의 장점이 있는 걸 알 수 있다.
3줄 정리
- 적절한
mini-batch사이즈를 선택해서 1번 학습의 속도를 높인다. Adam같은 최적화 알고리즘으로 학습을 최적화해 수렴속도를 높인다.- 경우에 따라
Learning rate decay로 빠르게 이동 후optima근처에서 속도를 낮추어 수렴한다.

댓글남기기