[DLS]Hyperparameter Tuning, Regularization and Optimization(1)

Andrew Ng 교수님의 Coursera - Deep Learning Specialization 두번째 강의입니다. 이번 게시글은 Regularization을 다룹니다.

Train/dev/test sets

적절한 학습을 위해 하나의 거대한 Data set을 여러 부분으로 나누어 활용한다.

• Train set
  • 학습을 위한 데이터
• Dev set
  • Hold-out cross validation, Development set 이라고도 불린다.
  • 개발 과정에서 train한 모델들의 성능을 검증하기 위한 데이터
• Test set
  • 학습과 검증 등에 전혀 사용되지 않은 unbiased 데이터
  • 최종적으로 모델의 성능을 평가

Dev set의 점수를 통해 더 나은 모델을 선택하기 때문에 모델이 dev에 fitting 될 수 밖에 없다. 따라서 최종적인 평가는 전체 과정에 사용된 적이 없는 모델 입장에서 처음보는 데이터(Test set)를 사용해서 이루어져야한다.

예전에는 70%/30% or 60%/20%/20% 의 비율로 나누었지만, 현대의 big data 시대에서는 dev와 test의 비율을 줄였다. 단순히 평가를 위함이기 때문에 백만의 데이터가 있을 때 만개 정도의 dev와 test면 충분하다.

Bias and Variace

Train set error	Dev set error	Type
1%	11%	high variace
15%	16%	high bias
15%	30%	high bias & high variance
0.5%	1%	low bias & low variace(good!)

• bias: 정답과 얼마나 차이가 나는지의 정도
• varaince: 다양한 데이터 세트에 대해 일정한 결과가 나오는지에 대한 정도

Machine Learning Methodology

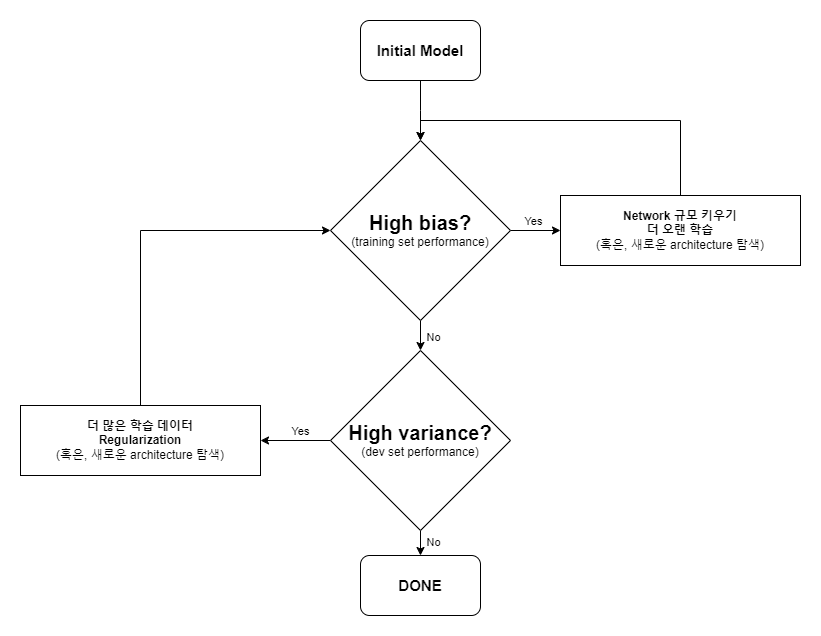
먼저 overfitting이든 아니든 트레이닝 셋의 오류를 줄여 bias를 낮춘다. 이후 variance를 고려하여 overfitting을 제거한다.

Regularization

정규화를 통해 overfitting을 막고 varaince를 줄일 수 있다.

\[cost\,function = \frac{1}{m}\sum_{i=1}^mL(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m}\sum_{l=1}^L\|\mathbf{w}^{[l]}\|_{2}^{2}\]

• labda $\lambda$: regularization hyperparameter

추가된 수식은 일종의 $Complexity$ 이다. weight의 값들이 클 수록 모델이 복잡하다고 여기고(즉, 데이터를 과하게 해석한 overfitting) cost를 높게 설정한다.

정규화를 적용했을 때 gradient는 아래와 같이 변한다.

\[d\mathbf{w} = (backprop) + \frac{\lambda}{m}\mathbf{w}\]

이는 업데이트 과정에서 아래와 같이 적용된다.

\[\mathbf{w} = \left(1 - \frac{\alpha\lambda}{m} \right)\mathbf{w} - \alpha \cdot (backprop)\]

이러한 결과 때문에 L2 norm regularization은 weight decay라고도 불린다.

정규화는 cost function에 정규화 항을 추가함으로써 이루어진다!

L2 Regularizaton

주로 L2가 사용된다.

\[\frac{\lambda}{2m}\|\mathbf{w} \|_2^2 = \frac{\lambda}{2m}\sum_{i=1}^{n_x} \mathbf{w}_{i}^{2}\]

제곱으로 인해 미분 시 2가 추가되므로 분모에 2를 추가해 연산의 편의를 맞춘다.

matrix에 대한 L2 norm은 Frobenius norm(프로베니우스 노름)라고 부른다.

\[\| \mathbf{w^{[l]}} \|_{2}^{2} = \| \mathbf{w^{[l]}} \|_{F}^{2} = \sum_{i=1}^{n^{[l]}}\sum_{j=1}^{n^{[l-1]}} \left(\mathbf{w}_{ij}^{[l]}\right)^2\]

L1 Regularization

\[\frac{\lambda}{m}\| \mathbf{w} \|_1 = \frac{\lambda}{m}\sum_{i=1}^{n_x} |\mathbf{w}_{i}|\]

L2 보다 sparsity, 성기다. 몇몇 파라미터가 0이 되어버리기 때문에 그런 목적이 아니라면 잘 안쓰인다.

L1 이 성긴(sparsity) 이유

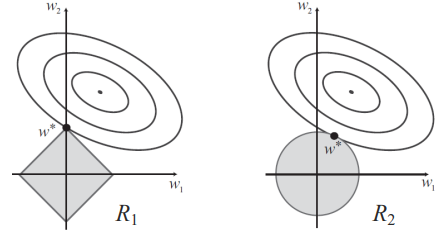
먼저 타원을 보면, 같은 타원에 있는 점(w1, w2)은 같은 loss 값을 만들어 낸다. 정규화를 적용한다면 해당 loss들에 정규화 값을 더하게 된다. 비용을 최소화하기 위해선 손실이 같을 때 정규화 값을 가장 작게 만들어야한다.

마름모와 원을 보면, 각각 L1과 L2의 같은 $complexity$를 만들어내는 위치이다. 즉, 어떤 loss 값(특정 타원)이 있을 때 정규화한 값을 최소화하기 위해서는 가장 작은 마름모 혹은 원을 선택해야한다.

따라서 loss의 타원과 정규화의 마름모(L1) 혹은 원(L2)이 한점에서 접하는 지점의 (w1, w2) 쌍을 골라야한다. 이러한 점을 고려했을 때 L2의 가장 작은 원은 원의 둥근 면에서 만나므로 weight들이 0으로 가는 경우는 드물지만, L1의 가장 작은 마름모의 경우 주로 꼭짓점에서 타원과 접하게 된다.

이런 이유로 L1 정규화는 파라미터들이 0으로 변하는 경우가 많음을 기하학적으로 이해할 수 있다.

왜 정규화가 overfitting을 막을까?

정규화를 통해 weight이 0에 가까워지고 몇몇 뉴런이 0에 근접하면 비활성화 된거 같은 효과를 보일 수 있다. 적은 뉴런의 모델은 단순하다는 뜻이며 결과도 단순하게 된다.

tanh 같은 활성화 함수에서는 weight이 작아 0에 근접한 값이 나온다면 tanh의 0과 근접한 부분들은 선형적인 직선처럼 생겼으므로 선형 활성화 함수처럼 된다. 따라서 모델이 단순해 진다.

“진리는 단순하다”라는 말이 있다. 그럴듯하게 설명하는 모델 중 가장 단순한 걸 골라야 과적합을 피할 수 있다. 이러한 이유로 weight 값들 최대한 작게 만들어 단순하게 만든다.

Dropout Regularization

매 batch 마다 각 뉴런들을 확률적으로 비활성화(dropout to zero) 시켜서 값을 계산한다. 뉴런이 유지될 확률 keep_prob이 있을 때, 모든 뉴런에 대해 독립적으로 keep_prob 확률로 유지된 뉴런에 대해서만 계산한다.

학습 과정에서만 Dropout을 사용하고 test 과정에서는 Dropout을 사용하지 않는다.

테스트에서의 dropout은 불필요한 noise만 만들 뿐이다.

Inverted dropout

• 남아 있는 각 뉴런의 출력 값에 keep_prob을 나누어 참여된 뉴런의 값을 증가시켜 보정한다.
• Dropout을 적용하면 몇몇 뉴런이 계산에서 제외 되었으므로 출력 값이 작아질 것이다.
• 이 문제를 해결하고 기대 출력 값을 동일하게 유지하기 위해 Inverted dropout을 적용해야 한다.

Dropout의 의미

Dropout을 쓰면 랜덤하게 뉴런이 사라지므로 특정한 뉴런에만 의존하지 않고 전체적으로 weight이 spread 된다. 특정 값만 커지지 않고 고르게 분포하게 만드는 점에서 L2 penalty와 비슷한 매커니즘을 가진다.

computer vision 분야에서는 input pixel이 많고 항상 데이터가 부족하기에 overfitting이 잦다. 따라서 dropout을 거의 항상 사용하게 된다. Dropout은 결국 과적합을 피하기 위해서 사용하는 것이므로 과적합이 존재할 때만 사용하자.

Early Stop

train loss와 dev loss가 함께 감소하다가 dev loss가 늘어나는 시점(overfitting이 발생)에 일찍 멈추는 것.

좋은 방법이지만 위의 머신러닝 흐름도 처럼 bias와 variance를 분리하지 못한다. 항상 varainace를 작게하며 정확도를 높게(bias를 작게)해야하므로 두 요소가 함께 고려해야하고 이는 알고리즘의 최적화를 약간 어렵게 만든다.

따라서 L2 정규화를 적용하는 식으로 variance를 줄이는 게 좋다.(이 방법은 $\lambda$ 하이퍼파라미터 튜닝을 해야하는 일이 추가되는 단점이 존재하긴 한다.)

단점을 많이 적었지만 Early stop은 많이 사용하는 좋은 방법이다!

Normalization

input 값들을 각각 표준화 하자. W에 대한 비용함수를 좀 더 symmetric 하게 만들 수 있다. 어떤 input의 범위는 500 ~ 1000 인 반면, 어떤 input은 0 ~ 1이면 weight에 scale 이 포함된다. 이는 weight에 대해 손실 함수를 비대칭적으로 만들고 학습을 어렵게 만든다. 따라서 Normalization 이 필요해진다.

\[\mathbf{x} := \frac{\mathbf{x} - \mu}{\sigma}\]

• $\mu$: 평균
• $\sigma$: 표준편차

Vanishing/Exploding gradients

layer가 많아질수록 입력에서 출력층까지 더 많은 Weight이 곱해지게 된다. 문제를 단순화 시켜 바라볼때 weight들이 W > 1 이라면 지수적으로 켜져 exploding 할 것이고, W < 1 이라면 지수적으로 작아져 0으로 vanishing 되어버릴 것이다. 이는 gradient descent 과정에도 동일하게 적용되므로 이 경우 학습이 매우 천천히 일어나게 되는 문제가 발생한다.

해결법: Weight Initailization 잘하기

입력은 Normalization이 되어 $N(0, 1)$의 정규분포일것이다. weight 초기화로 np.random.randn()을 하면 마찬가지로 $N(0, 1)$의 분포에서 선택되고 이게 $n^{[l-1]}$개가 더해지니 해당 뉴런의 출력은 $N(0, n^{[l-1]})$ 가 된다. 따라서 np.random.randn() * $np.sqrt(\frac{1}{n^{[l-1]}})$ 으로 분산을 $\frac{1}{n^{[l-1]}}$로 만들어 준다.

• Relu의 경우는 분산을 $\frac{2}{n^{[l-1]}}$로 한다. 음수의 경우 0으로 버려지기 때문에 기대값이 절반이므로 2를 추가적으로 곱해야한다.