[DLS]Convolutional Neural Networks(2)

Andrew Ng 교수님의 Coursera - Deep Learning Specialization 네번째 강의입니다. 객체 감지, 얼굴인식, YOLO, U-Net, Neural style transfer 등을 다룹니다.

Object localization

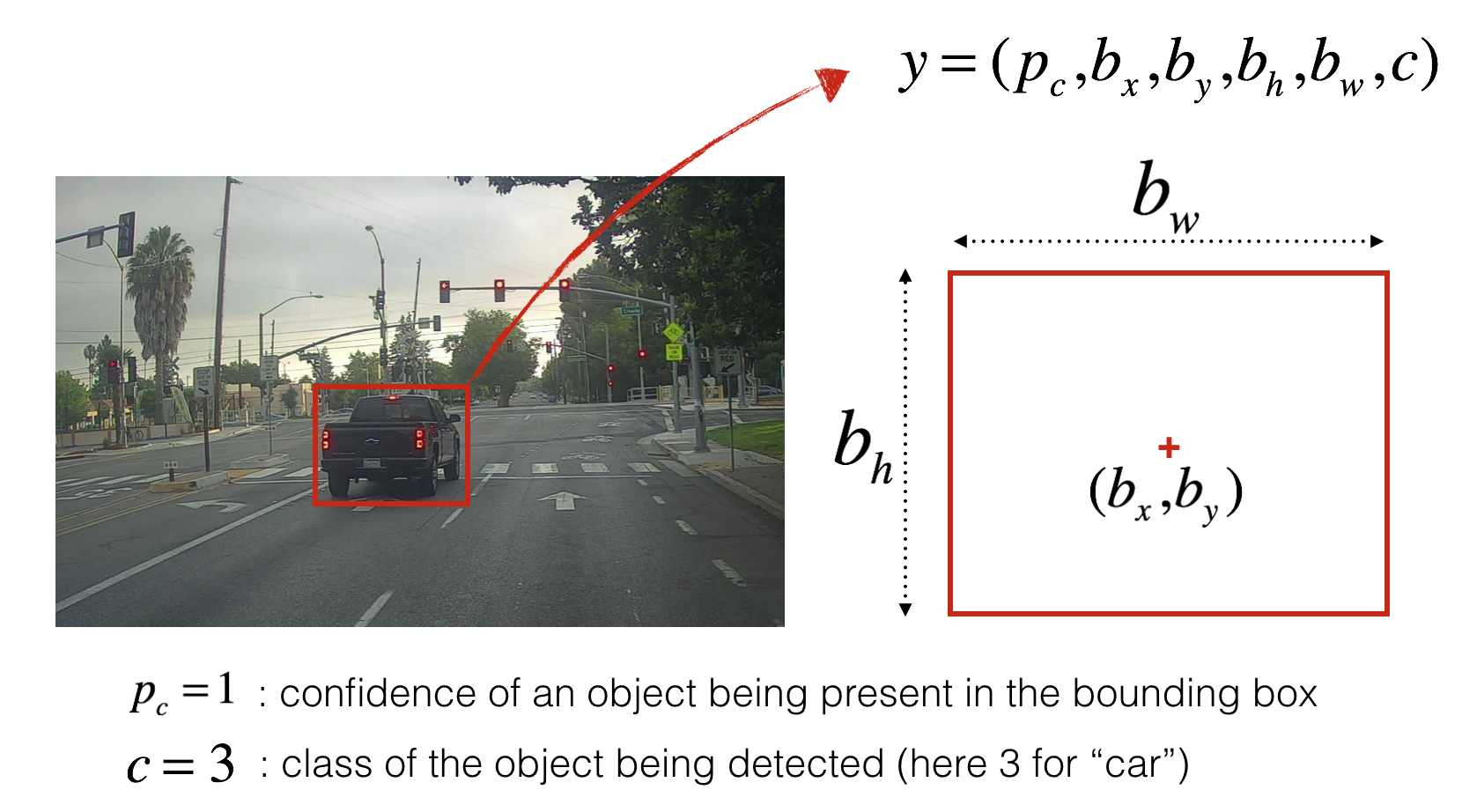
softmax로 이미지를 분류하는 것 만이 아닌 이미지 상의 객체 영역(bounding box)을 찾아낸다.

$b_x$, $b_y$, $b_h$, $b_w$의 출력 값이 존재하며 (bx,by)는 객체의 중심위치, bw, bh는 bounding 박스의 크기를 결정한다.

Convolution implementation of sliding windows

$b_x$, $b_y$, $b_h$, $b_w$를 사용하는 방식이 아니라 평범한 ConvNet 분류기를 사용한다.

이미지의 일부분을 잘라서 ConvNet을 적용하는 방식이지만, ConvNet을 반복 연산하는 것이 아닌 한번에 연산이 가능하다.

가령 window의 픽셀이 32x32라면 32x32로 학습시킨 ConvNet 모델의 파라미터를 가지고 영역을 찾아야하는 이미지(256x256)에 적용한다. 그러면 각 window의 위치들에 대한 예측을 한번에 수행할 수 있다.

• 여기서 일반적인 ConvNet과 다르게 FC layer를 출력이 1x1xC 형태가 되는 ConvLayer로 사용해서 학습을 진행해야한다.
• FC Layer가 아닌 ConvLayer의 filter를 사용하기 때문에 입력 이미지가 커져도 파라미터가 사용가능하다.
• 훈련할때는 1x1x#class 의 Y 형태였지만 큰 이미지를 넣으면 WxHx#class의 형태로 각 window에 따라 classification 값이 나온다.

Sermanet et al., 2014, OverFeat: Integrated recognition, localization and detection using convolutional networks

YOLO(You Only Look Once)

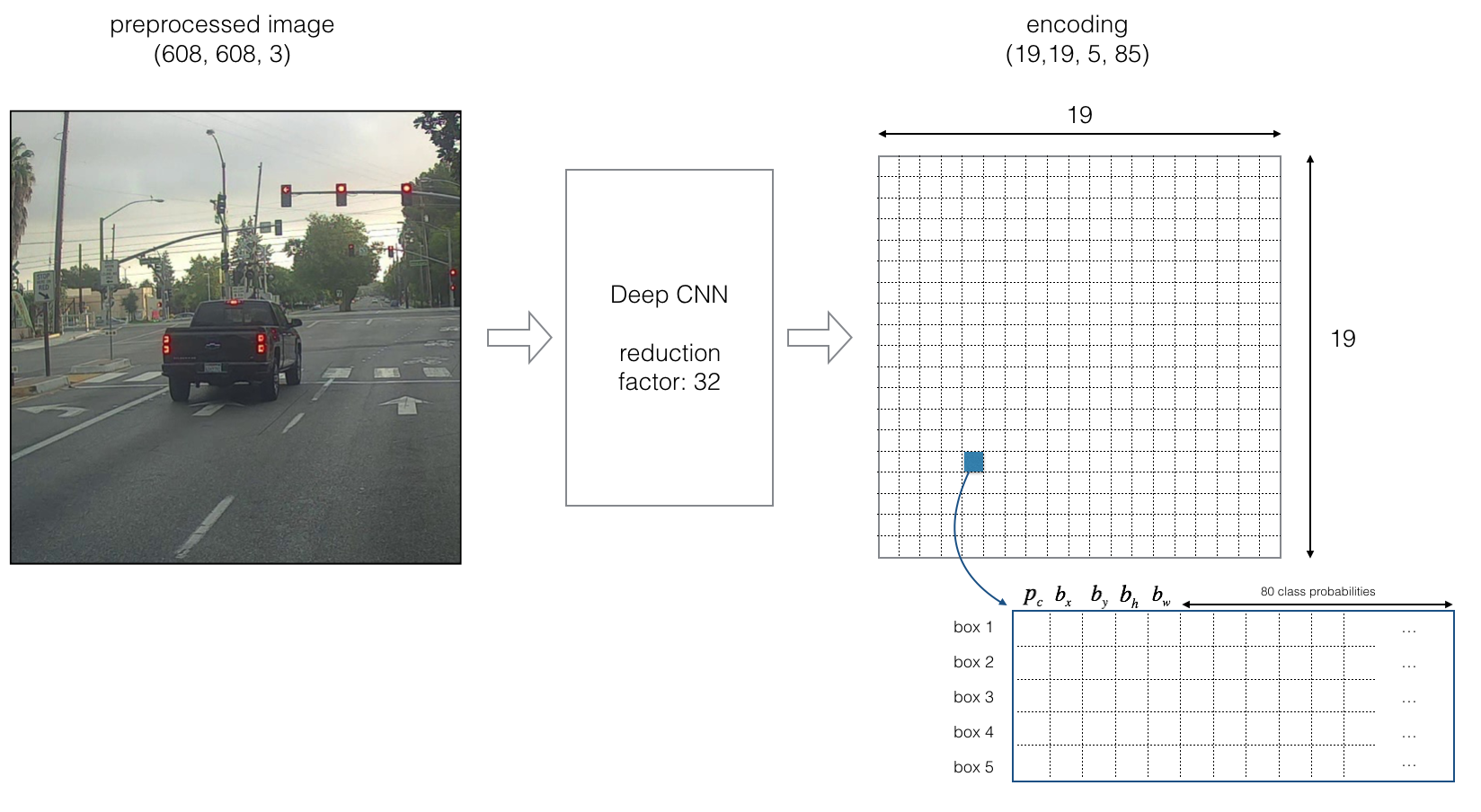
• 19 제곱의 격자로 나누어 한번에 확인한다.
• 객체의 중심 bx, by이 해당 격자의 알맞은 Anchor boxes로 감지된다.

Redmon et al., 2015, You Only Look Once: Unified real-time object detection

intersection over union(IoU)

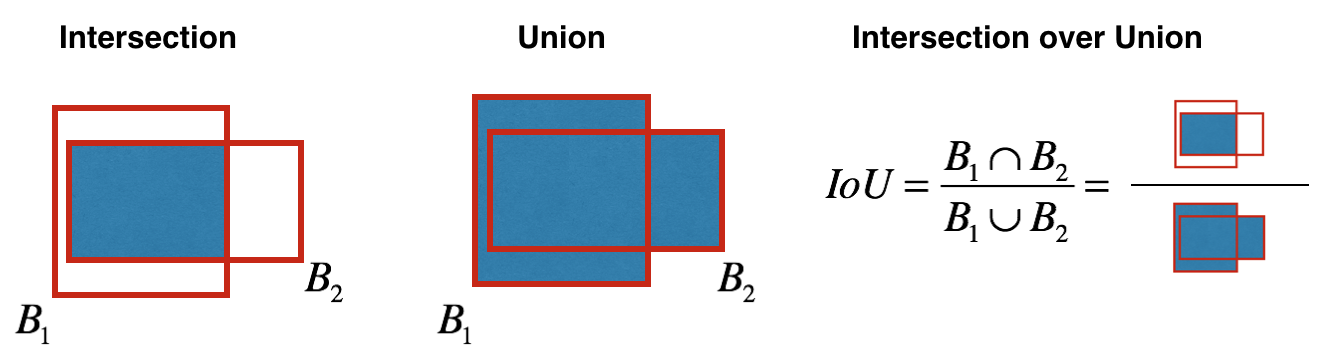
bounding box에 대한 평가를 한다. 예측된 영역과 실제 영역의 교집합(intersection)과 합집합(union)의 면적을 구한다. intersection size/union size를 IoU라고 부르며 0.5보다 크면 정답이라고 할 수 있다.

Non-max suppression

19의 제곱 만큼 격자가 존재하므로 한 객체를 인식한 여러 격자가 존재할 수 있다. 이때 $P_c$의 값(객체가 존재하는 확률)이 높은 것부터 채택하며 앞서 채택된 bounding box와 많이 겹치는 경우는 무시한다.

여기서 또한 IoU가 사용되며 해당 class의 기존 채택된 박스들과 IoU가 높다면 버려진다.

Anchor boxes

격자판만 사용한다면 한 격자에 단 하나의 객체만 파악이 가능하다. 여러 객체가 겹쳐 있을 수 있기 때문에 고안되었다. 상하로 길쭉한 객체와 좌우로 길쭉한 객체에 대해 각각 Anchor box를 설정해두면 적절한 anchor box로 들어가 여러개의 객체를 한 격자내에서 식별 가능해진다.

• 도입한 box 개수 만큼만 감지할 수 있다는 한계가 있다.
• 박스의 크기와 개수는 데이터에 대해 탐색적으로 설정한다.

R-CNN

이미지의 Region에 대해 각각 ConvNet을 적용하는 것이다. 이미지를 먼저 segmentation 알고리즘으로 영역을 분리하고 해당 영역에 대해 CNN으로 분류를 한다.

R-CNN의 장점은 정사각형의 window가 아닌 segmentation으로 적절한 region에 대해 알맞은 직사각형으로 분류할 수 있다는 것이다.

YOLO와 R-CNN은 각각 장단점이 있다.

U-Net(Image Segmentation)

ConvNet을 통해 이미지의 각 픽셀을 분류하여 형태를 완전히 찾아낸다. YOLO의 경우 bounding box였지만 U-Net은 segmentation이다.

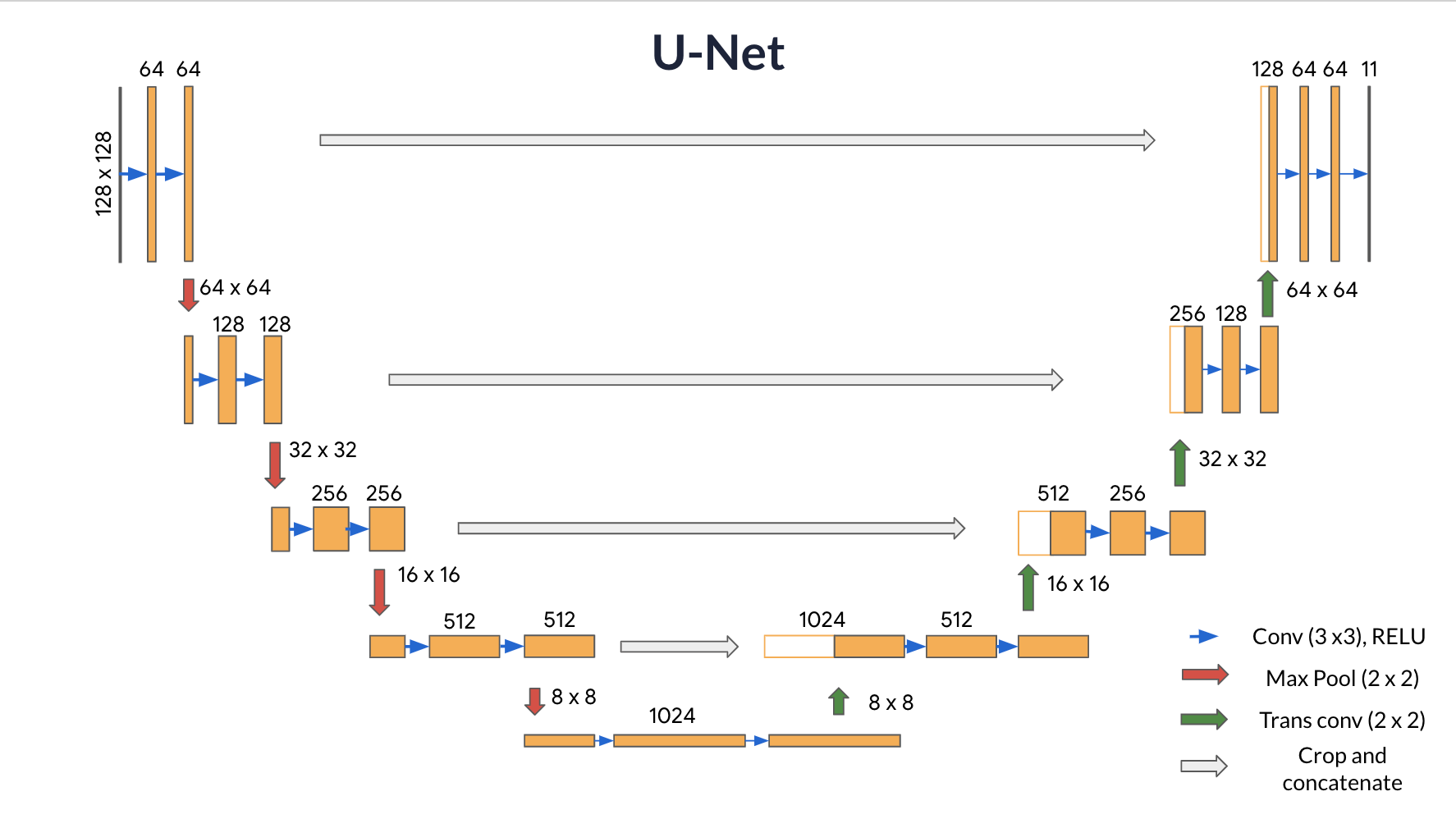
• 특징을 추출하기 위한 downsampling과 각 픽셀에 대해 분류하기 위한 upsampling 단계가 있다.
• 여기서의 skip connection은 ResNet과 다르게 더하는 게 아닌 concat이다.
• 마지막 출력 층은 클래스의 개수 만큼 채널이 존재해야한다.
• (참고)원핫 인코딩이 아닌 각 클래스, 정수로 되어 있을 때는 SparseCategoricalCrossentropy를 사용하면 편리하다

Transposed Convolution

Conv 연산으로 필터를 적용하면 크기가 줄어든다. 물론 여기서는 pooling으로 줄이긴 하지만 기존 convolution 연산으로는 이미지 크기를 늘릴 수가 없다.

transposed convolution이라는 색다른 연산을 사용함으로써 이미지 크기를 키운다.

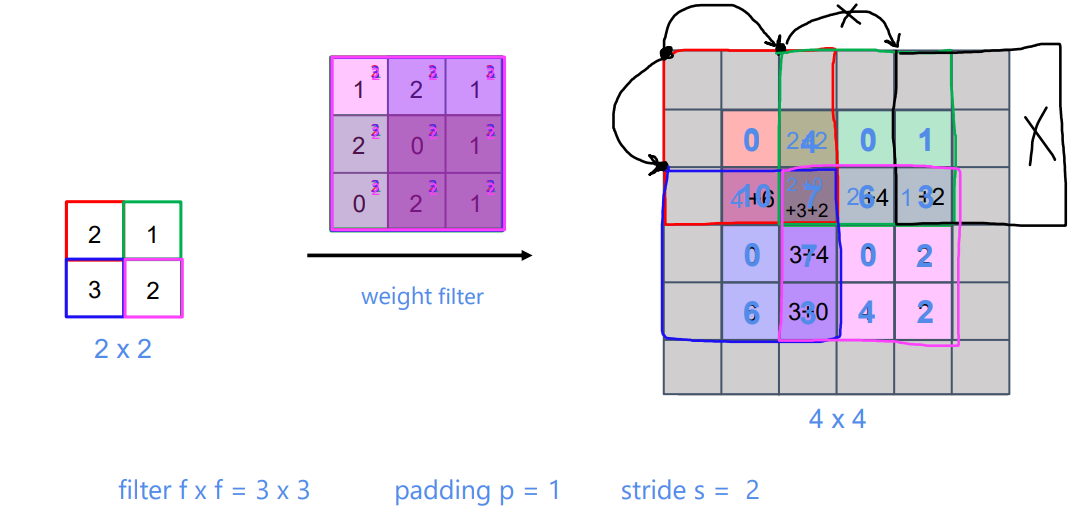
Face recognition

각 사람의 얼굴을 인식하여 어떤 사람인지 분류하는 문제이다. 기존 CNN 구조를 사용해도 되겠지만 각 사람에 대한 얼굴 사진 데이터가 수많이 필요하고, 사람이 추가되거나 빠질 시 네트워크를 재학습 시켜야 할 수 있다.

이러한 이유로 약간 다른 구조의 네트워크가 필요하다.

One shot Learning

하나의 데이터로 분류를 할 수 있도록 학습하는 걸 의미한다. 사람 얼굴 사진 한장으로 이사람이 맞는지 파악한다.

분류를 하는 모델이 아닌 두 개의 사진에서 각각 특징을 추출하고 특징의 유사도(similarity funtion)를 평가하게 만든다. 동일한 사람의 경우 특징의 차이가 0에 가깝게, 다른 사람의 경우 차이가 크게 만든다.

Siamese network(샴 네트워크)

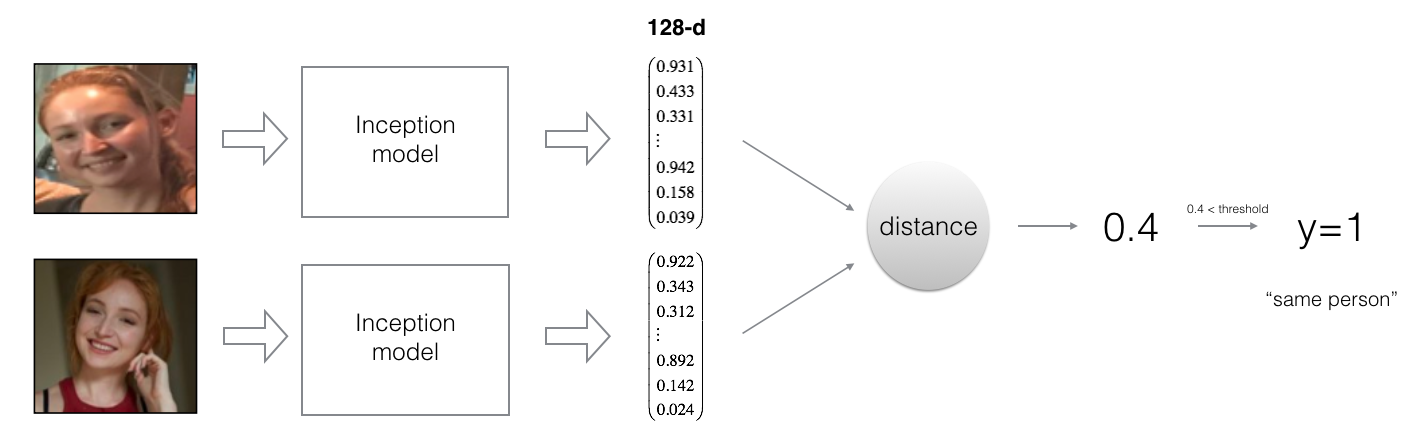
기존의 CNN 분류 모델을 중간 layer까지 잘라 같은 파라미터를 사용하도록(쌍둥이) 하여 두 이미지를 통과시킨다.

추출된 특징으로 거리를 계산한다.

Triplet Loss

\[\mathcal{J} = \sum^{m}_{i=1} max\left(\left[ \| f(A^{(i)}) - f(P^{(i)}) \|_2^2 - \| f(A^{(i)}) - f(N^{(i)}) \|_2^2 + \alpha \right], 0\right)\]

• A(Anchor): 대상
• P(Positive): 대상의 또 다른 이미지
• N(Negative): 대상이 아닌 이미지
• $f(A)$는 CNN을 통과한 A의 특징 벡터이다.
• $\alpha$는 threshold이자 margin으로 최소한 margin 만큼 특징 차이가 나야 하게 강제한다.
  • margin이 없으면 A, P, N에 대해 전부 0이 되어도 통과가 되어버린다.

Neural style transfer

신경망으로 이미지의 style을 변경하여 생성한다. 기존 처럼 모델의 parameter를 Gradient Descent 하는 것이 아닌, 생성되는 이미지의 픽셀을 Gradient Descent 하게 된다.

\[J(G) = \alpha J_{content}(C,G) + \beta J_{style}(S,G)\]

• C: Content image
• S: Style image
• G: Generated image

Content loss

ConvNet의 중간 레이어(적당한 특징)의 활성을 비교한다.

\[J_{content}(C,G) = \frac{1}{4 \times n_H \times n_W \times n_C}\sum _{ \text{all entries}} (a^{[l](C)} - a^{[l](G)})^2\]

Style Matrix(Gram Matrix)

히든 레이어의 채널들의 상관관계(corelation)를 style이라 정의하고 이를 비교할 것이다. 먼저 스타일(Gram)은 아래와 같이 계산된다.

\[\mathbf{G}_{gram} = \mathbf{A}_{unrolled} \mathbf{A}_{unrolled}^T\]

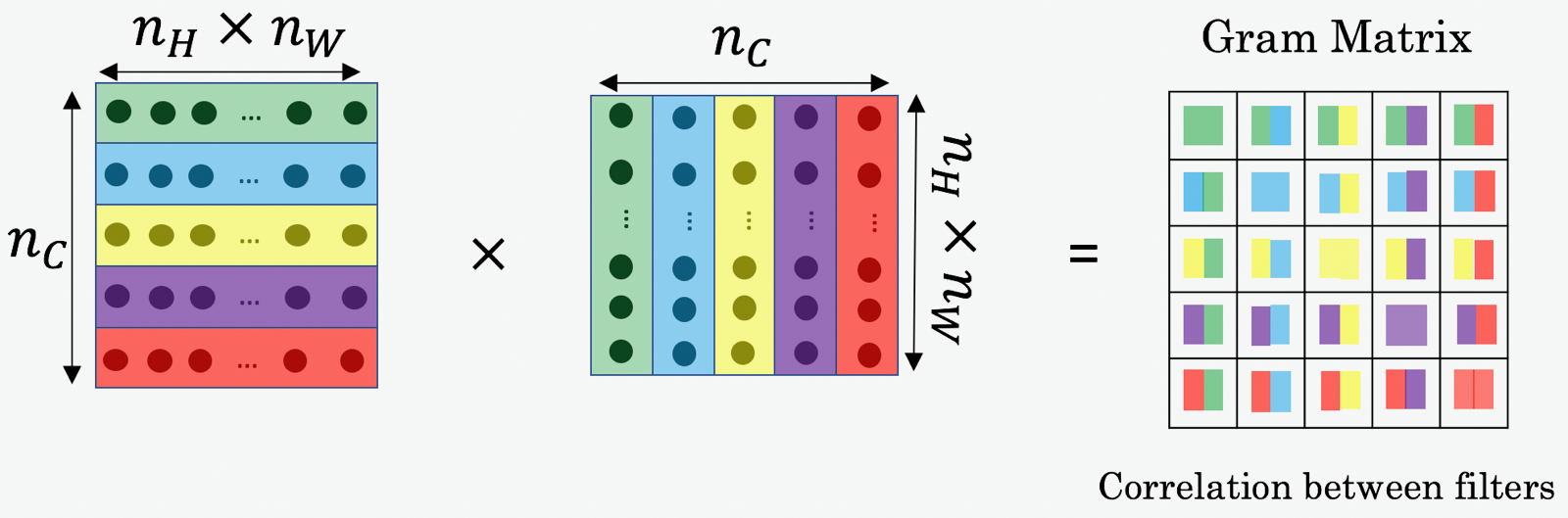
• $G_{(gram)ij}$ : i번째 채널과 j 번째 채널의 상관관계

Style loss

\[J_{style}^{[l]}(S,G) = \frac{1}{4 \times {n_C}^2 \times (n_H \times n_W)^2} \sum _{i=1}^{n_C}\sum_{j=1}^{n_C}(G^{(S)}_{(gram)i,j} - G^{(G)}_{(gram)i,j})^2\]

한 레이어에 대한 style loss는 위와 같이 계산된다. 이를 하나의 레이어만이 아닌 여러 레이어에 대해 적용하여 최종 loss를 계산한다.

\[J_{style}(S,G) = \sum_{l} \lambda^{[l]} J^{[l]}_{style}(S,G)\]

• $\lambda$는 각 레이어의 비율로 합쳐서 1이 나오는 하이퍼 파라미터이다.
  • $\sum_{l}^L\lambda^{[l]} = 1$