[DLS]Neural Networks and Deep Learning(2)

Andrew Ng 교수님의 Coursera - Deep Learning Specialization 첫번째 강의입니다. Neural Networks and Deep Learning는 이걸로 끝입니다.

Activation functions

이전 layer와의 선형 결합(WX + b) 후 적용하는 비선형 함수이다. 앞서서 logistic 회귀를 통해 sigmoid를 다루어 왔지만 종류는 더 많다.

절대적으로 좋은 활성화 함수는 존재하지 않는다. 상황에 맞게 실험적으로 좋은 활성화 함수를 찾아내야한다.

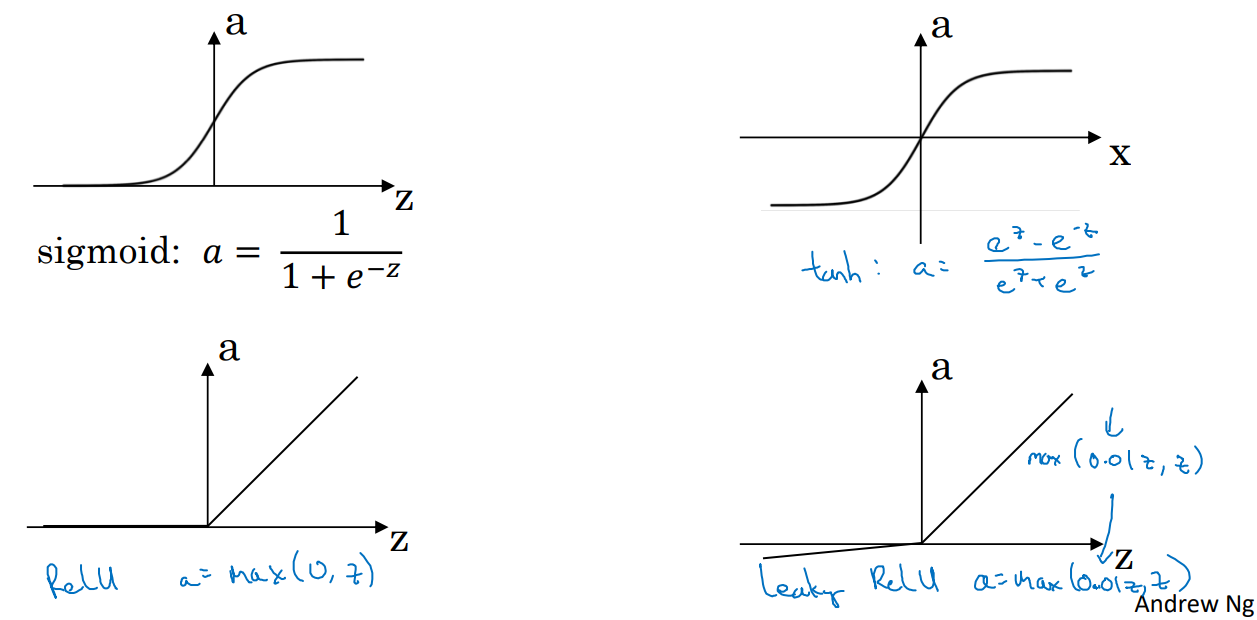
Sigmoid

\[\frac{1}{1+e^{-z}}\]

• 0 ~ 1의 범위를 갖는다.
• 로지스틱 회귀 같은 binary classification에서 결과값이 0 ~ 1 사이에 나와야하므로 이때 사용한다.

Hyperbolic Tangent

\[tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}\]

• sigmoid와 다르게 -1 ~ 1 범위를 갖는다.
• 이는 평균이 0이란 뜻으로 데이터를 centering하기 쉬워진다.
• sigmoid보다 대부분의 경우 성능이 좋다.

ReLU(Rectified Linear Unit)

\[max(0, z)\]

• 가장 많이 쓰이는 활성화 함수로 hidden layer에 뭘 쓸 지 모르겠으면 ReLU를 쓰자.

Leaky ReLU

\[max(0.01z, z)\]

• 음수일 때 0으로 값이 무시되는 경우를 방지하기 위해 고안.
• 나쁘지 않지만 그냥 ReLU도 잘 작동해서 ReLU 인기가 더 많음.
• 0.01 값은 적당히 바꿔도 된다.

Activation function을 사용해야하는 이유

활성 함수라는 비선형 함수가 존재하지 않는다면 hidden layer들의 의미가 사라진다. 각 layer의 weight들은 선형적으로 하나로 합쳐질 수 있고, 이는 아무리 많은 layer들이 존재하더라도 단일 layer와 동일해진다.

선형 활성 함수 $g(z) = z$를 사용하는 경우는 출력 값이 실수로 나와야하는 regression 문제에서의 output layer이다. 이러한 경우가 아닌 hidden layer에서는 거의 항상 비선형 활성 함수가 필요하 다.

Derivatives of Activation Functions

\[a = g(z)\]

Sigmoid

\[g(z) = \frac{1}{1+e^{-z}}\] \[\begin{aligned} g'(z) &= \frac{d}{dz} \left( \frac{1}{1 + e^{-z}} \right) \\ &= \left( \frac{1}{1 + e^{-z}} \right)^{2} \cdot e^{-z} \\ &= \left( \frac{1}{1 + e^{-z}} \right) \cdot \left( \frac{e^{-z}}{1 + e^{-z}} \right) \\ &= \left( \frac{1}{1 + e^{-z}} \right) \cdot \left( \frac{1 +e^{-z} - 1}{1 + e^{-z}} \right) \\ &= \left( \frac{1}{1 + e^{-z}} \right) \cdot \left( 1 - \frac{1}{1 + e^{-z}} \right) \\ &= a \cdot (1 - a) \end{aligned}\]

Hyperbolic Tangent

\[g(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}\] \[g'(z) = 1 - a^2\]

ReLU

z가 0 일때 미분 불가능인데, z가 정확히 0일 확률은 매우 낮다. 만약 0인 경우는 단순히 1로 직접 설정해주면 된다.

\[g(z) = max(0, z)\] \[g'(z) = \begin{cases} 0 & \text{if } z < 0 \\ 1 & \text{if } z \geq 0 \end{cases}\]

Leaky ReLU

\[g(z) = max(0.01z, z)\] \[g'(z) = \begin{cases} 0.01 & \text{if } z < 0 \\ 1 & \text{if } z \geq 0 \end{cases}\]

random initializaiton

로지스틱 회귀와 다르게 신경망은 0으로 초기화 하면 안된다. 로지스틱 회귀에서는 단일 출력 뉴런으로 연결되어 있어 상관없지만, 신경망의 경우 한 레이어에 여러개의 뉴런이 존재한다.

레이어들간은 fully connected 하기 때문에 해당 뉴런들이 동일한 함수를 가지게 되고, 가중치 업데이트가 동일하게 일어난다. 이런 경우는 다층 신경망의 장점을 살릴 수 없게 되기 때문에 동일한 값으로 초기화 해서는 안된다.

따라서 초기화는 random을 사용해서 수행된다. np.random.randn(input_size, hidden_size) * 0.01을 사용하여 표준 정규분포의 랜덤 값을 구하고 이에 0.01을 곱해 조정한다. 큰 값은 기울기가 0에 가까워지기 때문이다.

편향 bias의 경우는 weights가 랜덤하게 조정되었으므로 평범하게 0으로 초기화 해도 된다.

Deep Neural Network

layer가 여러개인 신경망도 앞서 서술한 방식들을 사용하면 구현할 수 있다. 각 layer들을 연결하는 $\left(n^{[l]} \times n^{[l - 1]}\right)$ 사이즈의 $W^{[l]}$ 들을 생성하고 신경망을 구축한다.

back propagation의 경우도 동일하게 chain rule을 사용하여 각 gradient들을 구할 수 있다.

deep NN을 사용하는 이유는 복잡한 함수를 만들 수 있기 때문이다.

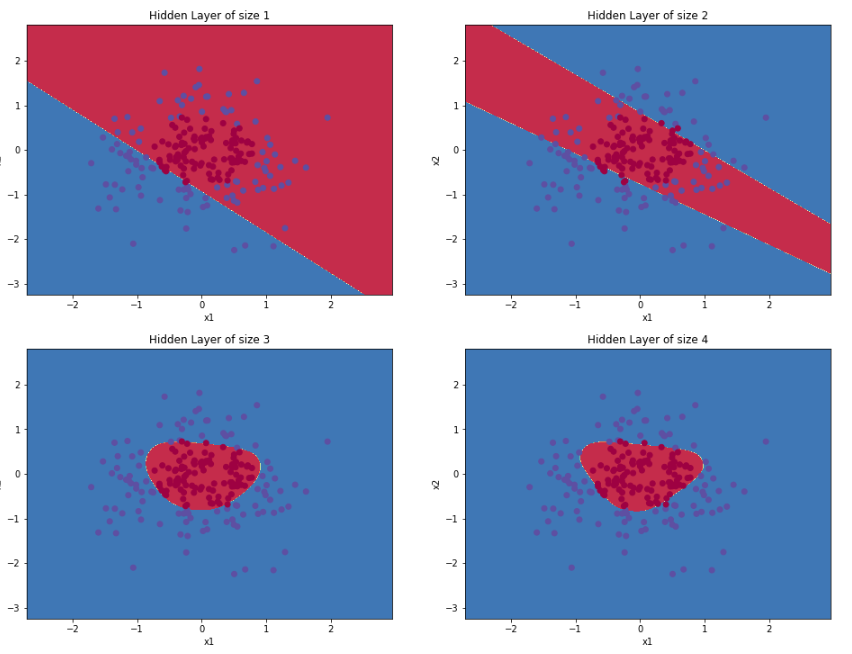
위 이미지는 이진 분류를 하는 로지스틱 회귀 모델의 예시이다. 1개의 출력 층만을 가지는 일반 로지스틱 회귀 모델의 경우 W 행렬이 한개 밖에 존재하지 않고 결과는 선형적으로 나온다.

즉, 레이어가 1개일때는 오직 직선(2차원에서, 3차원에서는 평면)으로 밖에 분류할 수 없다. 데이터에 맞는 복잡한 함수를 그리기 위해서는 신경망을 깊게 레이어를 구성하며, 각 레이어의 뉴런에 비선형 활성화 함수를 설정해야한다.