[DLS]Sequence Models(2)

Andrew Ng 교수님의 Coursera - Deep Learning Specialization 마지막 강의입니다. Natural Language Processing과 관련된 Word Embedding, Word2vec, GloVe 등을 배웁니다.

Word Embedding

각 단어를 N 차원의 공간의 특정 위치로 embedding 한다고 Word Embedding이라고 불린다.

Featurized representation

단어를 one-hot vector가 아닌 특징에 따라 벡터화 시킨다면 관련이 높은 단어를 유사하게 표현할 수 있다.

보통 50 ~ 1000 차원의 특징 벡터로 embedding 되어지고 같은 특징의 단어끼리 뭉치게 된다.

Embedding Matrix

#feature x #dictionary의 Matrix를 만든다. 이 Embedding Matrix에 특정 단어의 one-hot vector를 곱하면 해당하는 Embedding feature vector를 얻을 수 있게 된다.

실제로는 행렬 곱은 연산 비용이 커 E에 바로 인덱스로 접근해서 가져오게 된다.

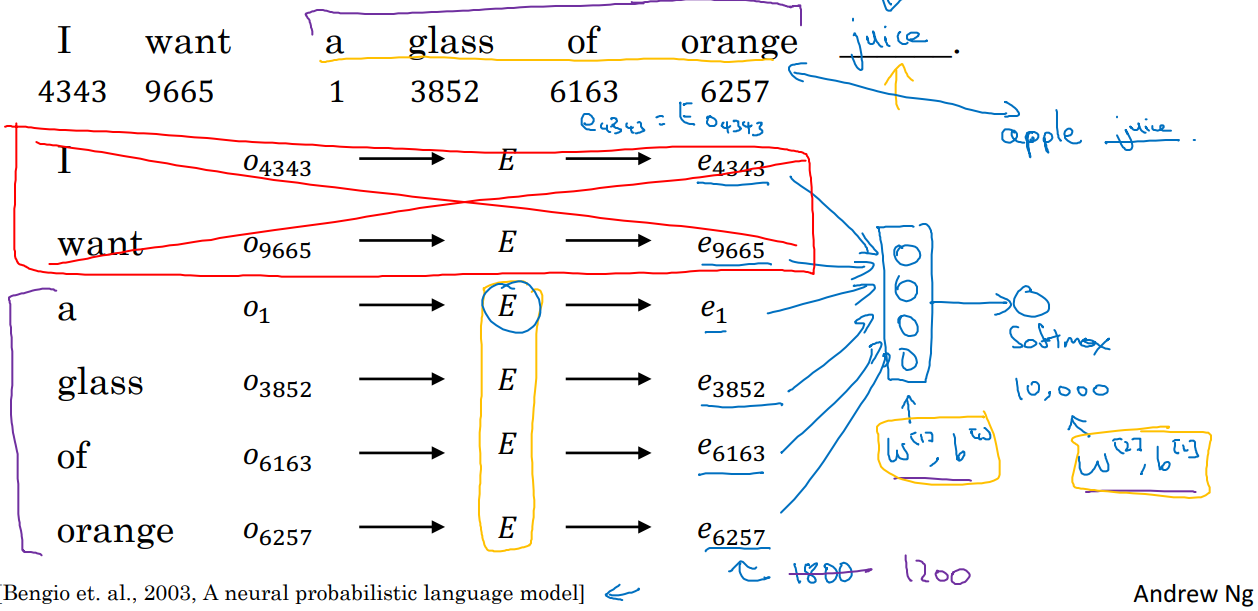
가장 기본적인 word embedding의 방법은 fixed historical window를 사용해 앞 n개의 단어(예: 4개)를 보고 뒤 단어를 예측하게 하며 E를 찾아내는 것이다.

앞 context 단어들를 e vector로 변환 후, softmax로 다음에 올 가장 확률이 높은 단어를 찾기 위해 vocab 사이즈의 layer를 붙여 모델이 구성된다.

학습되는 파라미터는 E 행렬과 출력층으로 가는 weight가 있다. 이 과정을 통해 우리는 E를 만들 수 있다.

Visualizing word embeddings

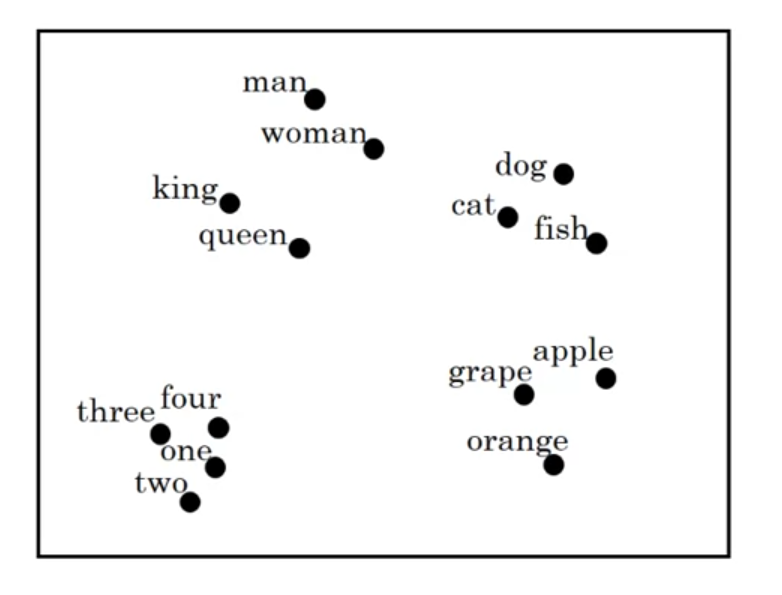
t-SNE같은 걸 사용해서 2차원 공간에서 단어 분포를 시각화해 확인 할 수도 있다.

• t-SNE: 비선형 차원 축소 기법

van der Maaten and Hinton., 2008. Visualizing data using t-SNE

Word2vec

Word2vec은 보다 더 간단하고 계산이 빠른 방법으로 제시되었다.

Skip-grams

fixed historical window가 아닌 Context 단어 근처의 한 단어를 예측할 목표(target)으로 삼고 학습하게 된다. 이 과정에서 몇 단어를 건너뛰고 선택이 가능하기 때문에 Skip gram 이라 불린다.

E를 적용한 embedding vector를 dense layer를 거쳐 vocab size 벡터로 변환 후 softmax를 적용해 예측한다.

\[\begin{aligned} softmax &= p(t | c) = \frac{e^{\theta_t^Te_c}}{\sum_{j=1}^{10000}{e^{\theta_j^Te_c}}} \\ e_c &= E \cdot o_c \\ \theta_t &= \text{parameter of output} \end{aligned}\]

• vocab size = 10,000으로 설정함

Negative Sampling

Skip-gram 모델은 softmax 과정을 거쳐야한다. vocab 사이즈가 10,000이 아니라 백만이 넘는 수준이 된다면 softmax 계산량이 엄청나게 증가하는 단점이 존재한다. 따라서 softmax를 통한 단어 예측이 아닌, sigmoid를 이용한 특정 단어가 맞는 지 아닌지의 문제로 변경한다.

orange - juice 라는 positive 쌍이 존재할 때, 랜덤한 다른 단어를 target으로 하는 negative 쌍들을 추가로 만든다.

• 작은 데이터 셋을 사용시 k(negative의 개수)를 5 ~ 20
• 큰 데이터 셋을 사용시 k를 2 ~ 5로 하는 걸 추천한다.

\[p(y = 1 | c, t) = \sigma(\theta_t^Te_c)\]

그렇게 생성된 학습 데이터를 사용하여 위 식을 학습하게 된다.

skip-gram의 경우 한번에 모든 vocab에 대한 $\theta$를 학습하며 softmax 연산을 해야했지만, Negative Sampling을 통해 vocab size 만큼의 Binary classification 문제로 변경하여 한번에 k+1개만큼만 학습하게 된다.

어차피 우리는 Embedding Matrix가 필요한 것이므로 이렇게 해도 괜찮다.

Sampling Method

sampling 할 때 완전히 무작위로 한다면, 자주 나오는 the, of, and, a 같은 것들의 비율이 커질 것이다. 따라서 아래 수식의 hueristic 방법을 사용한다.

\[P(w_i) = \frac{f(w_i)^{3/4}}{\sum_{j=1}^{10000}{f(w_j)^{3/4}}}\]

• $f$: empirical frequency

GloVe(Global Vectors for word representation)

\[\text{minimize}\sum_{i=1}^{10000}\sum_{j=1}^{10000}f(X_{ij})(\theta_i^Te_j + b_i + b'_j - logX_{ij})^2\]

• $X_{ij}$: i(Context)에서 j(target)가 나타난 횟수
  • target을 주변으로 잡으면 $X_{ij} = X_{ji}$
  • target과 context가 얼마나 관련이 있는지를 나타냄
• $f(X_{ij})$: $X_{ij}$가 0이면 0
  • $0 \cdot log0 = 0$
  • 최소 한번 이상의 관련이 있는 단어만 신경 쓴다는 의미

위 손실함수를 최소화함으로써 Embedding Matrix를 찾을 수 있다. 자세한 원리는 복잡해서 다루지 않았지만 더욱 간단해짐을 알 수 있다.

Word2vec 보다 덜 쓰이지만 훨씬 간단해서 좋아하는 사람들이 꽤 존재한다.

Pennington et. al., 2014. GloVe: Global vectors for word representation]