[Week 2]머신러닝 기초 이론 및 Transformer 기초

어떠한 작업 T에 대하여 경험 E 와 함께 성능 P 를 향상시키는 것을 머신러닝이라고 한다. <P, T, E>

• 작업(T): 주어진 이미지가 고양이인지 개인지 분류하는 작업
• 경험(E): 고양이와 개 이미지들로 이루어진 학습 데이터셋
• 성능(P): 이미지 분류 정확도

“Learning is any process by which a system imporves performance from experience” - Herbert Simon

최소 제곱법(OLS; Ordinary Least Squares)

선형 회귀 문제에서 파라미터(w, b)를 구하는 방법이다.

\[Cost(w, b) = \sum{(y_i- (wx_i + b))^2}\]

이를 최소화하기 위해 gradient descent 과정을 거쳐도 되지만 수식적으로 계산도 가능하다.

먼저 수식을 간략화 하기 위해 w와 b를 하나로 합쳐 $\beta$라고 표현한다.

\[\begin{aligned} \beta &= \left[ \begin{array}{c} w \\ b \end{array} \right] \\ \mathbf{x} &= \left[ \begin{array}{c} x & 1 \end{array} \right] \\ wx + b &= \mathbf{x}\beta \end{aligned}\]

위 식을 활용하면 아래와 같이 표현이 가능하다.

\[\begin{aligned} Cost(w, b) &= \sum{(y_i- (wx_i + b))^2} \\ &= \sum{(y_i- \mathbf{x}_i\beta)^2} \\ \end{aligned}\]

이제 미분 값이 0되는 지점의 $\beta$를 찾으면 된다.

\[\begin{aligned} \frac{\partial Cost(w, b)}{\partial \beta} &= \sum{-2\mathbf{x}_i \cdot (y_i- \mathbf{x}_i\beta)} \\ &= -2 X^T(Y-X\beta) \\ \end{aligned}\] \[\begin{aligned} -2X^T(Y-X\beta) &= 0 \\ X^TX\beta &= X^TY \end{aligned}\] \[\beta = (X^TX)^{-1}X^TY\]

이렇게 함으로써 원하는 파라미터를 계산 해낼 수 있다.

모델 평가 지표

MAE(평균 절대 오차)

각각의 차이를 더한다.

\[MAE = \frac{1}{n}\sum_{i=1}^n{|y_i - \hat{y}_i|}\]

MSE(평균 제곱 오차)

차이의 제곱을 더하기 때문에 데이터에 골고루 적용된다.

\[MSE = \frac{1}{n}\sum_{i=1}^n{\left(y_i - \hat{y}_i\right)^2}\]

RMSE(제곱근 평균 제곱 오차)

제곱근을 통해 오차를 원래의 단위로 변환하였다. 해석이 용이하기 때문에 모델 평가에서 많이 사용된다.

\[RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^n{\left(y_i - \hat{y}_i\right)^2}}\]

$R^2$(결정 계수)

모델이 종속변수 y의 변동성을 얼마나 잘 설명하는지를 나타내는 지표

0 ~ 1 범위를 가지며 1이면 완벽히 설명하는 것이다.

\[\begin{aligned} R^2 &= \frac{ESS}{TSS} \\ &= \frac{\sum_{i=1}^n{\left(\hat{y}_i - \bar{y}\right)^2}}{\sum_{i=1}^n{\left(y_i - \bar{y}_i\right)^2}} \\ &= 1 - \frac{RSS}{TSS} \\ &= 1 - \frac{\sum_{i=1}^n{\left(y_i - \hat{y}_i\right)^2}}{\sum_{i=1}^n{\left(y_i - \bar{y}\right)^2}} \end{aligned}\]

• TSS: Total Sum of Squares
  • 원래 데이터의 변동량
• ESS: Explain Sum of Squares
  • 모델이 표현하는 데이터(예측값)의 변동량
• RSS: Residual Sum of Squares
  • 예측값과 데이터와의 차이

KL Divergence(Kullback - Leibler)

실제 분포 P와 예측 분포 Q 간의 차이를 측정하여 모델을 평가하는 지표이다.

\[\begin{aligned} D_{KL}(P \parallel Q) &= \sum_{i} P(i) \log \frac{P(i)}{Q(i)} \\ D_{KL}(P \parallel Q) &= \int P(x) \log \frac{P(x)}{Q(x)} dx \end{aligned}\]

KL Divergence는 정보 이론의 엔트로피를 바탕으로 설계되었다.

• Entropy
  • $H(P) = - \sum_{i} P(i) \log P(i)$
  • 확률 분포 P에서 발생하는 정보량
• Cross Entropy
  • $H(P, Q) = - \sum_{i} P(i) \log Q(i)$
  • 실제 분포 P와 예측 분포 Q에 대해 발생하는 정보량

\[\begin{aligned} D_{KL}(P \parallel Q) &= \sum_{i} P(i) \log \frac{P(i)}{Q(i)} \\ &= H(P, Q) - H(P) \end{aligned}\]

즉, KL Divergence은 크로스 엔트로피의 값에서 엔트로피를 뺀 값이다. 크로스 엔트로피가 최소가 되는 지점은 P와 Q가 같은 것으로 이때 H(P)와 동일한 값을 가지게 된다. 따라서 KL Divergence의 최솟값은 0이 되어 평가 지표로 사용된다.

$D_{KL}(P \parallel Q)$는 $D_{KL}(Q \parallel P)$ 와 같지 않다!

Divergence는 발산이 아니라 “차이”를 의미하게 사용되었다.

numerical instability of Softmax

np.exp(2000) = np.inf이며 np.inf / np.inf = nan의 결과가 나온다.

따라사 softmax 함수의 오버 플로우 가능성을 막기 위해 최댓값을 빼주어 최댓값을 0으로 만들며 다른 값들을 전부 음수로 만든다.

\[\text{softmax}(x)_i = \frac{e^{x_i - \max(x)}}{\sum_j e^{x_j - \max(x)}}\]

이 경우 언더 플로우로 작은 값들이 0으로 간주될 수도 있지만, 이는 큰 문제가 되지 않는다.

데이터 정규화 기법

• PCA: 데이터를 정규화하여 zero-center을 만들고 축을 정렬
• whitening: covariance 행렬을 만듬

Attention based seq2seq

기존 encoder-decoder 구조의 RNN에서 Attention을 적용하여 모든 입력값의 hidden state를 보고 attention을 적용해 출력 값을 생성할 수 있다.

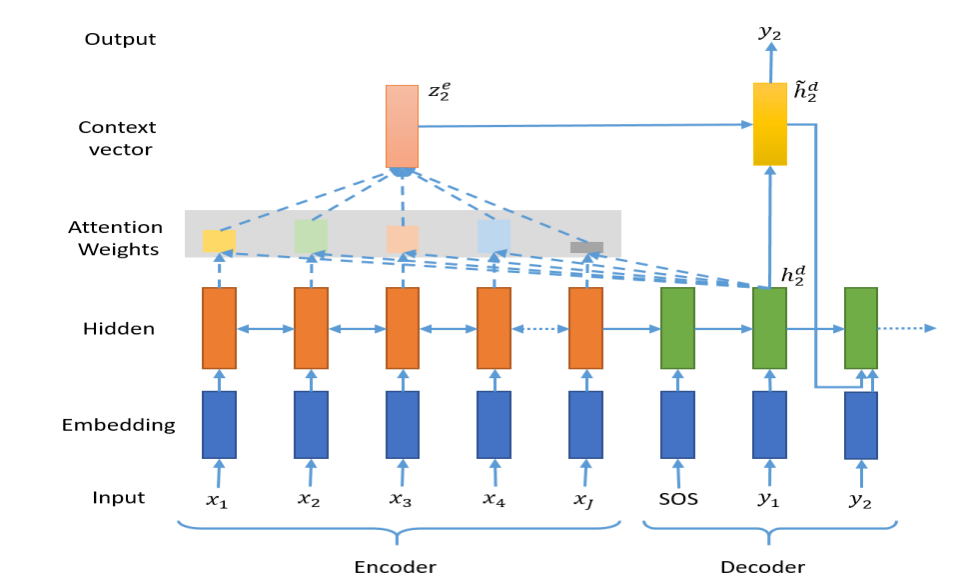
• query: Decoder의 hidden state
• Key, values: Encoder의 hidden state

이때, 각 decoder step의 output(hidden state)와 Attention 출력을 Concatenation 후 선형 변환을 통해 최종 예측 y를 계산할 수 있다.

coursera 강의에서 소개한 attention 모델은 query와 key를 concatenate 후 작은 NN을 거쳐 softmax를 거쳤었다.

그 외에도 transformer에서 소개한 것과 같이 위쪽 두번째 LSTM에서 이전 출력을 query로, 아래쪽 첫번째 LSTM의 값들을 key와 value로 표현하여 dot product Attention으로 사용이 가능하다.

Transformer를 사용한 분류/회귀 문제

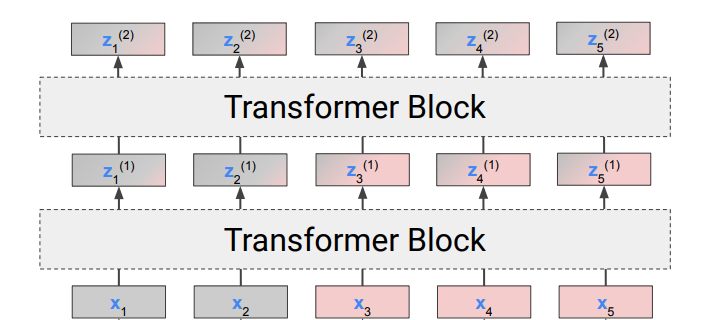
transformer는 self-attention을 사용하여 입력 시퀀스들을 병렬로 처리해 평행하게 출력을 만들어낸다. 즉, 입력 값의 시퀀스 길이만큼 출력이 나타난다.

이때 분류나 회귀 문제 같은 하나의 출력 값이 필요하다면 어떻게 해야할까?

Token Aggregation(Average Pooling)

가장 간단한 방법은 출력 토큰 값을 전부 더해 평균을 구하는 것이다. 그리고 linear 층을 통과해 classifier 문제를 해결할 수 있다.

하지만 시퀀스의 길이가 길어질수록 이는 좋은 방법이 아니다.

Classification Token [CLS]

[CLS] 라는 아무런 값을 가지지 않는 토큰을 입력 시퀀스의 맨 앞에 집어 넣는다.

[CLS]는 어떤 의미도 가지지 않기 때문에 transformer를 거치며 치우지지 않고 전체 문장에서 원하는 값을 추출할 수 있다.

BERT

BERT, Bidirectional Encoder Representations from Transformers는 인코더만을 사용하며 MLM(Masked Language Modeling)으로 양방향의 문맥을 학습하는 transformer 모델이다.

• 자기지도학습(Self-supervised Learning) 방식
  • MLM 기법이 자기지도학습이다.
• 인코더만을 사용

Input Embedding

• Token Embedding: 단어의 의미 정보
  • 특별한 토큰들이 존재하는데 CLS와 SEP가 있다.
    • [CLS]: 분류 토큰, 항상 맨앞에 존재
    • [SEP]: 한 문장이 끝날 때마다 존재하며 문장을 구분
• Segment embedding: 단어가 몇 번째 문장에 있는지 정보
• Position embedding: 단어의 위치 정보

MLM(Masked Language Modeling)

입력에서 임의로 15%의 토큰을 masking하여 없앤다.(특수한 토큰 [MASK]로 대체)

그리고 BERT가 이 문장에서 MASK 단어를 예측하도록하여 학습이 일어난다.(자기지도학습)

이 과정을 통해 BERT는 별도의 라벨링 없이 corpus들을 그대로 집어넣어 대용량 데이터를 학습할 수 있었고 시퀀스의 임베딩 표현에 있어서 뛰어난 성능을 발휘하였다.

이런 이유로 pretrained 된 BERT는 word embedding에서 기본으로 사용된다.

ViT(Vision Transformer)

이미지를 16x16 patch로 분할한다. 하나의 패치가 하나의 token으로 사용되어 transformer Encoder에 전달이 되고, 이미지를 분류하기 위해 [CLS] 토큰의 최종 출력 위에 MLP를 추가한다.

ViT는 CNN처럼 inductive bias(공간적 근접성 및 위치 불변성)를 가정하지 않기 때문에 학습에 있어서 극단적으로 큰 DataSet이 필요하다. 그렇더라도 충분한 데이터가 제공되면 CNN보다 복잡한 모델링이 가능하기 때문에 뛰어난 성능을 발휘할 수 있다.

ViT는 SOTA(State Of The Art;현재 가장 뛰어남)에 도달하였지만 학습 시간과 비용이 너무나 큰 문제가 존재한다.(8개의 TPUv3 로 300일의 학습이 진행되었다고 한다!)